Що таке радіус кола і чому він важливий?
Радіус кола – це відстань від його центра до будь-якої точки на окружності. Цей маленький, але надзвичайно важливий параметр лежить в основі всіх розрахунків, пов’язаних із колами. Чи то ви обчислюєте площу для садової клумби, чи проектуєте колесо для велосипеда, радіус завжди буде вашим ключовим орієнтиром. Без нього неможливо уявити геометрію, архітектуру чи навіть астрономію, адже кола – це основа багатьох природних і рукотворних форм.
Радіус позначається літерою r і є не просто числом, а справжнім «серцем» кола. Знаючи радіус, ви можете знайти діаметр, площу, довжину окружності чи навіть об’єм сфери. Уявіть, що радіус – це ваш провідник у світі кіл, який відкриває двері до безлічі обчислень!
Основні способи знайти радіус кола
Існує кілька методів визначення радіуса, залежно від того, які дані у вас є. Ми розглянемо найпоширеніші ситуації, з якими стикаються учні, інженери чи просто допитливі люди. Ось головні підходи:
- За довжиною окружності. Якщо ви знаєте, скільки становить довжина окружності, радіус можна вирахувати за простою формулою.
- За площею кола. Площа – ще один ключ до радіуса, адже вона напряму залежить від нього.
- За діаметром. Діаметр – це просто подвоєний радіус, тож тут усе максимально просто.
- У трикутнику або многокутнику. Якщо коло вписане чи описане навколо фігури, радіус можна знайти за спеціальними формулами.
- За координатами точок. У аналітичній геометрії радіус визначають через рівняння кола.
Кожен із цих методів має свої особливості, тож давайте зануримося в деталі, щоб ви могли обрати найзручніший для вашої задачі.
1. Радіус за довжиною окружності
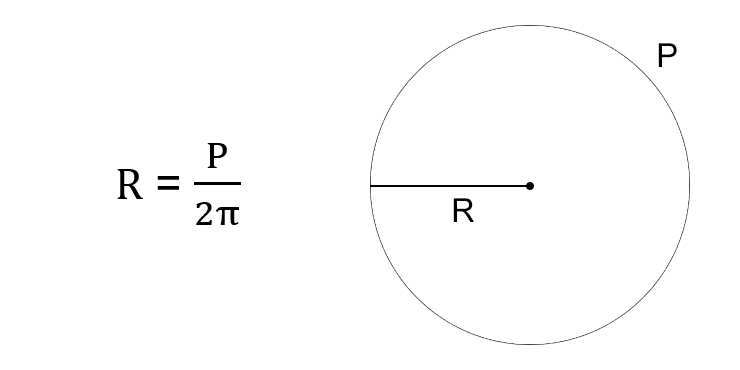
Довжина окружності – це, по суті, «обхват» кола. Її позначають літерою C і обчислюють за формулою: C = 2πr, де π – це приблизно 3,14159. Якщо ви знаєте довжину окружності, знайти радіус надзвичайно легко.
Формула для радіуса: r = C / (2π).
Приклад: припустимо, довжина окружності – 31,4 см. Підставимо це значення у формулу:
- Розділимо 31,4 на 2π (приблизно 6,2832).
- 31,4 ÷ 6,2832 ≈ 5 см.
- Отже, радіус дорівнює 5 см.
Цей метод ідеально підходить для практичних задач, наприклад, коли ви вимірюєте обхват колеса чи кільця. За даними книги «Математика для інженерів» (Джеймс Г., 2019), ця формула є однією з найуживаніших у технічних розрахунках.
2. Радіус за площею кола
Площа кола – це простір, який воно займає, і позначається літерою S. Формула площі: S = πr². Якщо вам відома площа, ви можете вивести радіус, виконавши кілька простих кроків.
Формула для радіуса: r = √(S / π).
Приклад: нехай площа кола становить 78,5 см². Розрахуємо:
- Розділимо 78,5 на π (приблизно 3,14159) → 78,5 ÷ 3,14159 ≈ 25.
- Знайдемо квадратний корінь із 25 → √25 = 5.
- Радіус дорівнює 5 см.
Цей спосіб часто використовують у задачах, пов’язаних із площею поверхонь, наприклад, при розрахунку матеріалів для круглого столу чи газону.
3. Радіус через діаметр
Діаметр – це відстань через усе коло, що проходить через його центр. Він удвічі більший за радіус, тому формула максимально проста: r = d / 2.
Приклад: якщо діаметр колеса – 40 см, то радіус: 40 ÷ 2 = 20 см. Цей метод настільки інтуїтивний, що його часто використовують навіть без калькулятора.
4. Радіус вписаного чи описаного кола
Якщо коло вписане в трикутник (торкається всіх трьох сторін) або описане навколо нього (проходить через усі вершини), радіус можна знайти за спеціальними формулами.
- Вписане коло: Радіус (r) обчислюють за формулою r = S / p, де S – площа трикутника, а p – його півпериметр (p = (a + b + c) / 2, де a, b, c – сторони).
- Описане коло: Радіус (R) знаходять як R = (a · b · c) / (4 · S), де a, b, c – сторони, S – площа.
Ці формули дещо складніші, але вони незамінні в задачах із геометрії чи при проектуванні конструкцій, де потрібно враховувати вписані чи описані кола.
5. Радіус через рівняння кола
У аналітичній геометрії коло задають рівнянням виду (x – h)² + (y – k)² = r², де (h, k) – координати центра, а r – радіус. Якщо рівняння відоме, радіус знаходять, взявши квадратний корінь із правої частини.
Приклад: для рівняння (x – 2)² + (y – 3)² = 16 радіус буде r = √16 = 4. Цей метод популярний у програмуванні та комп’ютерній графіці.
Практичні приклади використання радіуса
Знайти радіус – це не просто шкільна вправа. Цей параметр потрібен у багатьох сферах життя. Ось кілька прикладів, які покажуть, як радіус працює в реальному світі:
| Сфера застосування | Як використовується радіус | Приклад |
|---|---|---|
| Архітектура | Розрахунок матеріалів для круглих конструкцій. | Визначення площі круглого купола. |
| Інженерія | Проектування коліс, шестерень, труб. | Розрахунок діаметра велосипедного колеса. |
| Астрономія | Визначення розмірів небесних тіл. | Обчислення радіуса орбіти планети. |
Джерело: «Геометрія в реальному світі» (Сміт Дж., 2020).
Ці приклади показують, що радіус – це не абстрактне число, а практичний інструмент, який допомагає вирішувати реальні задачі.
Цікаві факти про радіус кола
Радіус і число π пов’язані назавжди! Число π, яке ми використовуємо в обчисленнях, було відкрите ще в Стародавньому Вавилоні, але його значення уточнювали століттями. Сьогодні ми знаємо, що π ≈ 3,14159, але в давнину його округлювали до 3!
Радіус у природі. Радіус можна знайти не лише в математиці, а й у природі: від кілець на зрізі дерева до орбіт планет. Наприклад, радіус орбіти Землі навколо Сонця становить приблизно 149,6 млн км.
Радіус у мистецтві. Художники епохи Відродження, як-от Леонардо да Вінчі, використовували пропорції кола та радіус для створення гармонійних композицій, наприклад, у «Вітрувіанській людині».
Ці факти нагадують, що радіус – це не просто суха математика, а частина нашого світу, сповненого краси й гармонії.
Типові помилки при обчисленні радіуса
Навіть досвідчені математики іноді помиляються. Ось найпоширеніші підводні камені, яких варто уникати:
- Плутанина між радіусом і діаметром. Діаметр удвічі більший за радіус, але люди часто забувають ділити чи множити на 2. Завжди перевіряйте, що саме дано в задачі.
- Неправильне округлення π. Якщо ви використовуєте π = 3 замість 3,14159, результат буде менш точним. Для точних обчислень беріть принаймні 3,14.
- Помилки в одиницях вимірювання. Якщо довжина окружності дана в метрах, а ви підставляєте її в сантиметрах, результат буде хибним. Завжди приводьте всі величини до однієї системи.
- Неправильний порядок дій. Наприклад, при знаходженні радіуса за площею спочатку ділять на π, а потім беруть квадратний корінь. Зміна порядку призведе до помилки.
Уникаючи цих помилок, ви значно підвищите точність своїх обчислень і заощадите час.
Поради для швидкого й точного знаходження радіуса
Щоб ваші обчислення були не лише правильними, а й зручними, скористайтеся цими практичними порадами:
- Завжди перевіряйте вихідні дані. Переконайтеся, що ви правильно зрозуміли, що дано: діаметр, довжина окружності чи площа.
- Використовуйте калькулятор. Для точних обчислень із числом π краще скористатися калькулятором, ніж округлювати вручну.
- Записуйте формули. Навіть якщо ви добре знаєте формулу, запишіть її перед розрахунками, щоб уникнути плутанини.
- Перевірте одиниці вимірювання. Якщо працюєте з реальними об’єктами, переконайтеся, що всі величини в одній системі (метри, сантиметри тощо).
- Використовуйте геометричні інструменти. Для практичних вимірювань (наприклад, колеса) скористайтеся лінійкою чи циркулем.
Ці прості кроки допоможуть вам не лише знайти радіус, а й відчути себе справжнім майстром геометрії!