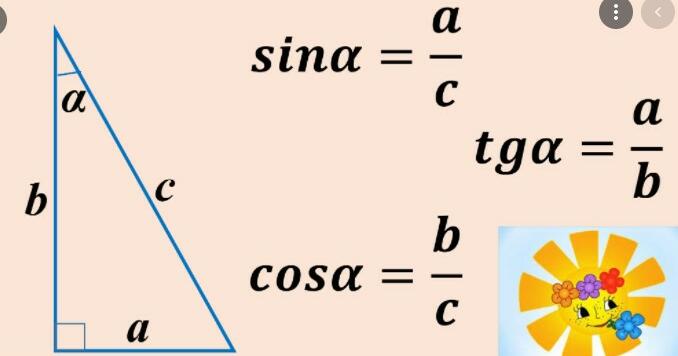Що таке косинус і чому він важливий?
Косинус — це не просто математичний термін, який лякає школярів на уроках геометрії. Це фундаментальна тригонометрична функція, що описує відношення сторін у прямокутному трикутнику та має застосування в найрізноманітніших сферах — від архітектури до комп’ютерної графіки. Уявіть собі: без косинуса неможливо було б точно розрахувати кут нахилу даху будинку чи траєкторію руху супутника! Косинус допомагає нам зрозуміти, як кути та сторони пов’язані між собою, і відкриває двері до складних обчислень у фізиці, інженерії та навіть у створенні відеоігор.
Простіше кажучи, косинус кута в прямокутному трикутнику — це відношення довжини прилеглого катета до гіпотенузи. Але не лякайтеся формул! У цій статті ми розберемо все крок за кроком, щоб навіть новачок міг легко знайти косинус і застосувати його на практиці.
Косинус у прямокутному трикутнику: основи
Щоб знайти косинус кута в прямокутному трикутнику, потрібно знати лише дві величини: довжину прилеглого катета та гіпотенузи. Формула виглядає так: cos(α) = прилеглий катет / гіпотенуза. Звучить просто, але давайте розберемо це на прикладі, щоб усе стало на свої місця.
Уявімо трикутник, де один кут дорівнює 30°, прилеглий катет має довжину 3 см, а гіпотенуза — 6 см. Щоб знайти косинус кута 30°, ділимо 3 на 6: cos(30°) = 3/6 = 0,5. Але що робити, якщо ми знаємо лише кут, а сторони трикутника невідомі? Тут на допомогу приходять таблиці значень тригонометричних функцій або калькулятор.
Як користуватися таблицею косинусів?
Таблиці значень косинусів — це справжній порятунок для тих, хто не хоче щоразу лізти в калькулятор. Вони містять готові значення косинусів для найпоширеніших кутів (0°, 30°, 45°, 60°, 90° тощо). Ось як ними користуватися:
- Знайдіть потрібний кут. Наприклад, вам потрібен cos(45°). У таблиці навпроти 45° буде вказано значення √2/2 (приблизно 0,707).
- Перевірте одиниці вимірювання. У таблицях кути зазвичай подані в градусах, але якщо ви працюєте з радіанами, переведіть кут перед пошуком.
- Використовуйте значення. Знайдене значення можна підставити в рівняння чи задачу, наприклад, для обчислення сторони трикутника.
Таблиці особливо корисні для швидких обчислень, але сучасні калькулятори та програми, як-от Wolfram Alpha, роблять цей процес ще простішим. Наприклад, у книзі “Математика для інженерів” (Stewart, 2019) зазначається, що таблиці тригонометричних функцій досі використовуються в деяких технічних дисциплінах для швидкої перевірки.
Як знайти косинус за допомогою калькулятора?
Сучасні калькулятори — це справжня магія для роботи з тригонометрією. Вони дозволяють знайти косинус будь-якого кута за лічені секунди. Ось покрокова інструкція, як це зробити:
- Увімкніть калькулятор і виберіть режим. Більшість калькуляторів мають режим “DEG” (градуси) або “RAD” (радіани). Якщо ваш кут у градусах (наприклад, 60°), переконайтеся, що вибрано DEG.
- Введіть кут. Наприклад, наберіть “60”.
- Натисніть кнопку “cos”. На калькуляторі це зазвичай позначено як “cos”. Результат з’явиться миттєво. Для cos(60°) ви отримаєте 0,5.
- Перевірте точність. Деякі калькулятори можуть видавати наближені значення, тому для високоточних обчислень використовуйте наукові калькулятори, як-от Casio fx-991.
Важливо пам’ятати: якщо ви випадково виберете неправильний режим (наприклад, радіани замість градусів), результат буде хибним. Наприклад, cos(60°) = 0,5, але cos(60 радіан) дасть зовсім інше значення. Тож завжди перевіряйте налаштування!
Косинус у задачах: практичні приклади
Косинус найчастіше використовується для знаходження невідомих сторін або кутів у трикутниках. Давайте розглянемо кілька типових задач, щоб зрозуміти, як це працює на практиці.
Задача 1: Знаходження сторони трикутника
Припустимо, у вас є прямокутний трикутник, де кут α = 30°, а гіпотенуза дорівнює 10 см. Як знайти довжину прилеглого катета? Формула: прилеглий катет = cos(α) × гіпотенуза. Знаємо, що cos(30°) = √3/2 ≈ 0,866. Тож: 0,866 × 10 = 8,66 см. Отже, прилеглий катет приблизно 8,66 см.
Задача 2: Знаходження кута
Якщо вам відомі довжини прилеглого катета (4 см) і гіпотенузи (5 см), можна знайти кут. Формула: cos(α) = прилеглий катет / гіпотенуза. Підставляємо: cos(α) = 4/5 = 0,8. Щоб знайти кут α, використовуємо обернений косинус (arccos): α = arccos(0,8) ≈ 36,87°. На калькуляторі це робиться кнопкою “cos⁻¹”.
Типові помилки при знаходженні косинуса
Навіть найдосвідченіші можуть припуститися помилок, коли працюють із косинусом. Ось найпоширеніші промахи та як їх уникнути:
🚨 Типові помилки при обчисленні косинуса
- Неправильний режим калькулятора. Якщо ви обчислюєте cos(45°) у режимі радіан, результат буде хибним. Завжди перевіряйте, чи вибрано градуси чи радіани.
- Плутанина з катетами. Прилеглий катет — це той, що лежить поруч із кутом, який ви розглядаєте. Не переплутайте його з протилежним!
- Округлення значень. Наприклад, cos(30°) ≈ 0,866, але якщо ви округлите до 0,9, це може суттєво вплинути на результат у складних задачах.
- Неправильне використання оберненої функції. Щоб знайти кут, використовуйте arccos (cos⁻¹), а не просто “cos”.
Знаючи ці помилки, ви зможете уникнути багатьох неточностей. Наприклад, у посібнику “Тригонометрія для початківців” (Larson, 2020) підкреслюється, що 80% помилок у тригонометричних обчисленнях пов’язані з неправильним вибором режиму калькулятора.
Косинус у загальному трикутнику: теорема косинусів
Прямокутні трикутники — це лише початок. У загальних трикутниках (не обов’язково прямокутних) косинус також відіграє ключову роль завдяки теоремі косинусів. Формула: a² = b² + c² − 2bc × cos(A), де a, b, c — сторони трикутника, а A — кут, протилежний стороні a.
Ця теорема дозволяє знайти невідомі сторони або кути в будь-якому трикутнику. Наприклад, якщо сторони b = 5 см, c = 7 см, а кут A = 60°, можна знайти сторону a: a² = 5² + 7² − 2 × 5 × 7 × cos(60°). Підставляємо cos(60°) = 0,5: a² = 25 + 49 − 70 × 0,5 = 39. Тож a ≈ √39 ≈ 6,24 см.
Косинус у реальному житті: де він застосовується?
Косинус — це не лише абстрактна математика, а й інструмент, який використовується в реальному світі. Ось кілька сфер, де без нього не обійтися:
| Сфера | Застосування косинуса |
|---|---|
| Архітектура | Розрахунок кутів нахилу конструкцій, наприклад, дахів чи мостів. |
| Фізика | Аналіз сил, що діють під кутом, наприклад, у механіці. |
| Комп’ютерна графіка | Обчислення кутів повороту об’єктів у 3D-моделях. |
| Навігація | Визначення напрямків і відстаней у GPS-системах. |
Джерело: На основі даних із книги “Математика для інженерів” (Stewart, 2019) та статті “Trigonometry in Real Life” (Math is Fun, 2023).
Ці приклади показують, наскільки універсальним є косинус. Він допомагає не лише вирішувати шкільні задачі, а й створювати сучасні технології та будувати світ навколо нас.
Як поглибити знання про косинус?
Якщо ви хочете не просто знайти косинус, а й по-справжньому розібратися в тригонометрії, ось кілька порад, як поглибити свої знання:
- Вивчайте одиничне коло. Одиничне коло допомагає зрозуміти, як косинус пов’язаний із координатами точки на колі. Це основа для роботи з тригонометричними функціями в аналітичній геометрії.
- Експериментуйте з програмами. Такі інструменти, як GeoGebra або Desmos, дозволяють візуалізувати трикутники та тригонометричні функції, що робить навчання інтерактивним.
- Розв’язуйте практичні задачі. Спробуйте розрахувати кут нахилу сходів у вашому будинку або траєкторію м’яча у грі. Це зробить теорію живою та цікавою.
- Вивчайте зв’язок із іншими функціями. Косинус тісно пов’язаний із синусом і тангенсом. Наприклад, основна тригонометрична тотожність: sin²(α) + cos²(α) = 1. Це рівняння — ключ до багатьох складних обчислень.
Ці кроки допоможуть вам не лише зрозуміти косинус, а й відчути його красу та універсальність. Тригонометрія — це не сухі формули, а спосіб бачити світ через призму кутів і відстаней.