Чому теорема Піфагора – ключ до розв’язання?
Теорема Піфагора – це фундаментальний інструмент у геометрії, який допомагає знаходити невідомі сторони прямокутного трикутника. Якщо ви знаєте довжини гіпотенузи та одного катета, знайти квадрат іншого катета – справа кількох простих обчислень. Ця теорема не лише корисна для шкільних задач, а й застосовується в реальному житті, наприклад, у будівництві чи навігації. У цій статті ми детально розберемо, як за теоремою Піфагора знайти квадрат катета, коли відомі гіпотенуза та інший катет, із покроковими поясненнями, прикладами та порадами, щоб ви могли впевнено розв’язувати такі задачі.
Що каже теорема Піфагора?
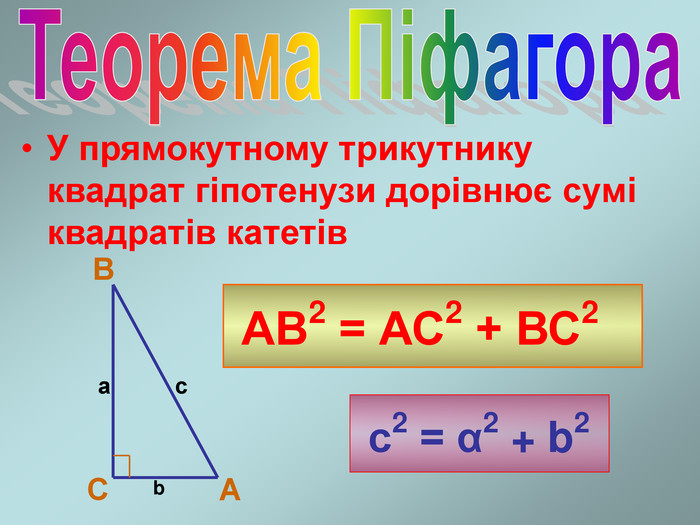
Теорема Піфагора стосується прямокутних трикутників, де один кут дорівнює 90°. Вона формулюється так:
a² + b² = c²
де:
- a і b – катети (сторони, що прилягають до прямого кута).
- c – гіпотенуза (сторона навпроти прямого кута, найдовша).
Якщо відомі гіпотенуза c і один катет, наприклад, a, ми можемо знайти квадрат іншого катета b², використовуючи цю формулу. Давайте розберемо, як це зробити.
Покроковий алгоритм знаходження квадрата катета
Щоб знайти квадрат катета за теоремою Піфагора, виконайте ці прості кроки. Припустимо, нам відомі гіпотенуза c і катет a, а ми шукаємо квадрат катета b².
Крок 1: Запишіть формулу теореми Піфагора
Формула виглядає так:
a² + b² = c²
Наше завдання – знайти b², тобто квадрат невідомого катета.
Крок 2: Висловіть квадрат невідомого катета
Щоб знайти b², перенесемо відомий член формули в іншу сторону рівняння:
b² = c² – a²
Ця формула дозволяє обчислити квадрат катета b, якщо ми знаємо квадрати гіпотенузи c і катета a.
Крок 3: Підставте відомі значення
Підставте числові значення c і a у формулу. Наприклад, якщо гіпотенуза c = 5, а катет a = 3, обчислимо:
b² = 5² – 3²
b² = 25 – 9
b² = 16
Отже, квадрат катета b² дорівнює 16.
Крок 4: Перевірте результат
Щоб переконатися, що обчислення правильні, підставте знайдене b² назад у теорему Піфагора:
a² + b² = c²
Для нашого прикладу:
3² + 16 = 5²
9 + 16 = 25
25 = 25
Рівняння виконується, тож результат правильний.
Крок 5 (опціонально): Знайдіть катет b
Якщо задача вимагає не лише квадрат катета, а й саму його довжину, обчисліть квадратний корінь із b²:
b = √b²
У нашому прикладі:
b = √16 = 4
Отже, катет b дорівнює 4.
Приклади розв’язання задач
Щоб закріпити розуміння, розглянемо кілька прикладів із різними значеннями.
Приклад 1: Проста задача
Гіпотенуза трикутника c = 13, катет a = 5. Знайдіть квадрат катета b².
- Формула: b² = c² – a²
- Підставимо: b² = 13² – 5²
- Обчислимо: b² = 169 – 25 = 144
- Перевірка: 5² + 144 = 25 + 144 = 169 = 13²
Відповідь: b² = 144.
Приклад 2: Десяткові значення
Гіпотенуза c = 10.2, катет a = 6.8. Знайдіть квадрат катета b².
- Формула: b² = c² – a²
- Підставимо: b² = 10.2² – 6.8²
- Обчислимо: 10.2² = 104.04, 6.8² = 46.24
- b² = 104.04 – 46.24 = 57.8
- Перевірка: 46.24 + 57.8 = 104.04 = 10.2²
Відповідь: b² = 57.8.
Приклад 3: Задача з коренем
Гіпотенуза c = √50, катет a = 5. Знайдіть квадрат катета b².
- Формула: b² = c² – a²
- Підставимо: b² = (√50)² – 5²
- Обчислимо: (√50)² = 50, 5² = 25
- b² = 50 – 25 = 25
- Перевірка: 25 + 25 = 50 = (√50)²
Відповідь: b² = 25.
Типові помилки при обчисленнях
Новачки можуть припускатися помилок, які призводять до неправильних результатів. Ось як їх уникнути:
🚨 Типові помилки при використанні теореми Піфагора
- Плутанина з гіпотенузою: Гіпотенуза завжди найдовша сторона. Якщо ви помилково візьмете катет за гіпотенузу, c² – a² може дати від’ємне число, що неможливо.
- Неправильне обчислення квадратів: Перевіряйте розрахунки, особливо з десятковими числами. Наприклад, 6.8² = 46.24, а не 46.2.
- Пропуск перевірки: Завжди підставляйте результат назад у формулу a² + b² = c², щоб упевнитися в правильності.
- Ігнорування одиниць: Якщо сторони задані в сантиметрах, квадрат буде в см². Дотримуйтесь одиниць вимірювання.
Щоб уникнути помилок, виконуйте обчислення покроково й перевіряйте кожен етап.
Практичні поради для розв’язання
Щоб знаходження квадрата катета було легким і точним, дотримуйтесь цих порад:
- Використовуйте калькулятор: Для десяткових чисел або великих значень калькулятор заощадить час і зменшить ризик помилок.
- Малюйте трикутник: Схематичне зображення допоможе чітко визначити, яка сторона є гіпотенузою, а які – катетами.
- Перевіряйте розмірність: Гіпотенуза завжди більша за катет. Якщо a > c, ви помилилися в ідентифікації сторін.
- Тренуйтеся: Розв’яжіть кілька задач із різними числами (цілими, дробовими, коренями), щоб набити руку.
Порада: якщо результат b² від’ємний, перевірте, чи правильно ви визначили гіпотенузу – вона завжди найбільша сторона.
Застосування в реальному житті
Теорема Піфагора, зокрема знаходження квадрата катета, має практичне значення в багатьох сферах:
- Будівництво: Визначення довжини діагоналі фундаменту чи стіни для перевірки прямого кута.
- Навігація: Обчислення відстані між двома точками на карті, якщо відомі їхні координати.
- Дизайн: Розрахунок розмірів меблів чи декоративних елементів із трикутними формами.
Наприклад, якщо ви хочете перевірити, чи стіна утворює прямий кут із підлогою, виміряйте гіпотенузу та один катет і обчисліть квадрат іншого катета, щоб переконатися в правильності конструкції.
Цікаві факти про теорему Піфагора
Теорема Піфагора не лише практична, а й має багату історію:
📐 Цікаві факти про теорему Піфагора
- Стародавнє походження: Теорему знали ще вавилоняни за 1000 років до Піфагора, але він систематизував її в VI столітті до н.е.
- Універсальність: Теорема працює не лише в пласкій геометрії, а й у тривимірному просторі, наприклад, для обчислення діагоналей куба.
- Піфагорійські трійки: Набори чисел, як-от (3, 4, 5) чи (5, 12, 13), що задовольняють a² + b² = c², називаються піфагорійськими трійками.
Ці факти додають теоремі Піфагора глибини, показуючи її значення в математиці та історії.