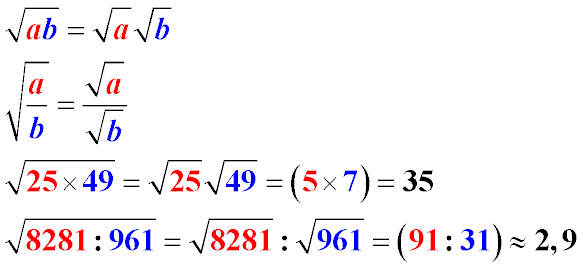Обчислення кореня — це захоплива подорож у світ математики, де числа відкривають свої таємниці. Чи то квадратний корінь для шкільного завдання, чи кубічний для інженерних розрахунків, ця навичка потрібна кожному, хто прагне розгадати числові головоломки. У цій статті ми розберемо, як обчислити корінь різними методами, пояснимо складні концепції простими словами та поділимося практичними порадами.
Що таке корінь у математиці?
Корінь числа — це значення, яке, якщо піднести його до певного степеня, дає вихідне число. Наприклад, квадратний корінь із 16 дорівнює 4, бо 4² = 16. Це ніби пошук “першоджерела” числа, його математичної основи. Корені бувають різних видів: квадратні, кубічні, четвертого степеня тощо, залежно від показника степеня.
У математиці корінь позначається символом √ (радикал), а число під ним називають підкореневим виразом. Якщо показник кореня не вказаний, мається на увазі квадратний корінь (√x = x^(1/2)). Для інших коренів, наприклад кубічного, пишуть ³√x.
Розуміння коренів важливе не лише в математиці, а й у фізиці, інженерії та навіть програмуванні. Наприклад, у графіці квадратний корінь використовується для обчислення відстаней, а в статистиці — для стандартного відхилення.
Види коренів: від квадратного до n-го
Щоб обчислити корінь, потрібно знати, з яким типом ви працюєте. Кожен вид має свої особливості, і ми розберемо їх детально.
Квадратний корінь
Квадратний корінь (√x) — найпоширеніший тип. Він шукає число, яке при множенні на себе дає x. Наприклад, √25 = 5, бо 5 × 5 = 25. Важливо: для додатних чисел квадратний корінь має два значення (позитивне і від’ємне), але в шкільних задачах зазвичай беруть лише позитивне.
Кубічний корінь
Кубічний корінь (³√x) шукає число, яке при множенні на себе тричі дає x. Наприклад, ³√8 = 2, бо 2 × 2 × 2 = 8. На відміну від квадратного, кубічний корінь визначений і для від’ємних чисел: ³√(-8) = -2.
Корінь n-го степеня
Корінь n-го степеня (ⁿ√x) узагальнює концепцію. Він шукає число, яке при піднесенні до n-го степеня дає x. Наприклад, ⁴√16 = 2, бо 2⁴ = 16. Такі корені рідше зустрічаються в шкільних програмах, але важливі в вищій математиці та техніці.
Методи обчислення кореня: від простого до складного
Існує кілька способів обчислити корінь: від інтуїтивного підбору до складних алгоритмів. Ми розглянемо найпопулярніші методи, щоб ви могли вибрати той, який вам до душі.
Метод підбору (для ідеальних квадратів)
Для чисел, які є ідеальними квадратами (4, 9, 16, 25 тощо), можна просто згадати, яке число в квадраті дає цей результат. Наприклад, щоб знайти √49, підберіть: 7 × 7 = 49, отже, √49 = 7.
Цей метод простий, але працює лише для невеликих чисел і ідеальних квадратів. Для √50 він уже не підійде, бо 50 — не ідеальний квадрат.
Факторизація
Факторизація допомагає знайти корінь, розкладаючи число на прості множники. Наприклад, для √144:
- Розкладіть 144: 144 = 2 × 2 × 2 × 2 × 3 × 3.
- Згрупуйте пари однакових множників: (2 × 2) × (2 × 2) × (3 × 3).
- Візьміть по одному множнику з кожної пари: 2 × 2 × 3 = 12.
- Отже, √144 = 12.
Цей метод зручний для великих чисел, але вимагає знання простих чисел і терпіння.
Метод послідовного наближення (алгоритм Ньютона)
Для чисел, які не є ідеальними квадратами, використовують алгоритм Ньютона. Це ітераційний метод, який наближає значення кореня. Формула: xₙ₊₁ = (xₙ + a/xₙ)/2, де a — число, з якого беремо корінь.
Приклад для √50:
- Візьміть початкове наближення, наприклад, x₀ = 7 (бо 7² = 49 ≈ 50).
- Обчисліть: x₁ = (7 + 50/7)/2 = (7 + 7.14)/2 ≈ 7.07.
- Повторіть: x₂ = (7.07 + 50/7.07)/2 ≈ 7.071.
- Після кількох ітерацій отримаємо √50 ≈ 7.071.
Цей метод точний, але потребує обчислень. Сучасні калькулятори використовують схожі алгоритми.
Використання калькулятора або програм
Найшвидший спосіб — скористатися калькулятором або програмами, як-от Python чи Excel. У Python квадратний корінь обчислюється функцією math.sqrt(x), а для n-го кореня — x**(1/n). Наприклад:
- √25:
import math; print(math.sqrt(25))→ 5.0. - ³√8:
print(8**(1/3))→ 2.0.
Цей метод ідеальний для швидких розрахунків, але не допомагає зрозуміти процес.
Практичні приклади обчислення кореня
Щоб закріпити знання, розглянемо кілька прикладів із реального життя.
Приклад 1: Площа квадрата
У вас є квадрат із площею 81 см². Яка довжина його сторони? Оскільки S = a², то a = √S = √81 = 9 см. Отже, сторона квадрата — 9 см.
Приклад 2: Об’єм куба
Об’єм куба — 125 см³. Яка довжина ребра? Об’єм куба V = a³, тому a = ³√V = ³√125 = 5 см.
Приклад 3: Відстань у тривимірному просторі
У програмуванні для обчислення відстані між точками (x₁, y₁, z₁) і (x₂, y₂, z₂) використовують формулу: d = √((x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)²). Наприклад, для точок (1, 2, 3) і (4, 6, 8): d = √((4-1)² + (6-2)² + (8-3)²) = √(9 + 16 + 25) = √50 ≈ 7.07.
Порівняння методів обчислення кореня
Щоб вибрати найкращий метод, порівняємо їх за ключовими критеріями.
| Метод | Складність | Точність | Застосування |
|---|---|---|---|
| Підбір | Низька | Тільки для ідеальних квадратів | Шкільні завдання |
| Факторизація | Середня | Висока для цілих чисел | Великі числа |
| Алгоритм Ньютона | Висока | Дуже висока | Точні розрахунки |
| Калькулятор | Низька | Найвища | Швидкі обчислення |
Джерело: математичні довідники та онлайн-ресурси (mathworld.wolfram.com).
Вибір методу залежить від ваших цілей. Для швидкості — калькулятор, для розуміння — факторизація чи алгоритм Ньютона.
Цікаві факти про корені
Корені — це не лише математика, а й частина нашого життя. Ось кілька захопливих фактів, які розкривають їхню магію.
- 🌟 Золотий перетин. Квадратний корінь із 5 (√5 ≈ 2.236) є частиною формули золотого перетину φ = (1 + √5)/2, яке використовується в мистецтві та архітектурі.
- 🔢 Ірраціональні числа. Корінь із 2 (√2 ≈ 1.414) — перше відоме ірраціональне число, відкрите піфагорійцями. Воно викликало справжній переворот у математиці!
- 🚀 Космічні розрахунки. У навігації космічних апаратів корені використовуються для обчислення траєкторій і відстаней у тривимірному просторі.
- 🎵 Музика і корені. Частоти нот у музичних акордах пов’язані через корені, наприклад, √2 визначає інтервали в рівномірно темперованому строї.
Типові помилки при обчисленні кореня
Навіть досвідчені математики можуть припуститися помилок. Ось найпоширеніші промахи та як їх уникнути.
- Ігнорування від’ємного кореня. Для квадратного кореня додатного числа є два значення: ±√x. Наприклад, при розв’язанні x² = 16 забувають, що x = ±4.
- Неправильне спрощення. Деякі плутають √(a + b) із √a + √b. Наприклад, √(9 + 16) ≠ √9 + √16, бо √25 = 5, а 3 + 4 = 7.
- Помилки в десяткових наближеннях. При ручних обчисленнях округлення на ранніх етапах може призвести до неточностей.
Щоб уникнути помилок, завжди перевіряйте результат: піднесіть знайдений корінь до відповідного степеня і порівняйте з вихідним числом.
Поради для ефективного обчислення кореня
Хочете стати майстром обчислення коренів? Ось кілька практичних порад, які зроблять процес легшим і приємнішим.
- 📝 Починайте з оцінки. Для √50 уявіть, що 7² = 49, а 8² = 64. Значить, корінь між 7 і 8, що допоможе з наближенням.
- 🛠️ Використовуйте технології. Для складних чисел застосовуйте Python або Excel, щоб заощадити час.
- ✅ Перевіряйте результат. Завжди підносьте знайдений корінь до степеня, щоб переконатися в правильності.
- 📚 Вивчайте таблицю квадратів. Запам’ятавши квадрати чисел від 1 до 20, ви швидше знаходите корені для невеликих чисел.
Обчислення кореня — це не просто математична вправа, а спосіб розвинути логіку та аналітичне мислення. Незалежно від того, чи ви школяр, чи інженер, ці методи та поради допоможуть вам розкрити магію чисел. Практикуйте, експериментуйте та насолоджуйтеся процесом!