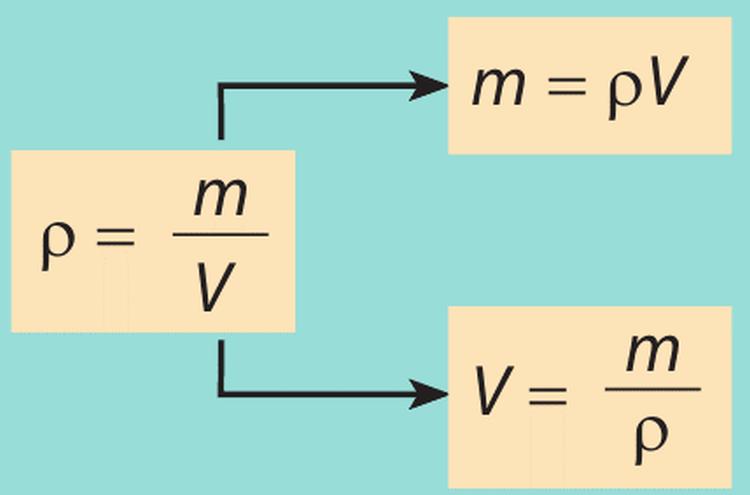
Що таке об’єм і чому він важливий?
Об’єм — це міра того, скільки простору займає об’єкт у тривимірному світі. Уяви собі коробку з-під взуття, наповнену цукерками: об’єм покаже, скільки цих цукерок туди поміститься! Цей параметр важливий у математиці, фізиці, інженерії та навіть у повсякденному житті — від планування переїзду до розрахунку кількості води в басейні. Розуміння, як знайти об’єм, відкриває двері до практичних рішень і допомагає бачити світ більш структуровано.
Об’єм вимірюється в кубічних одиницях: кубічних метрах (м³), сантиметрах (см³), літрах (1 л = 1000 см³) тощо. У кожній задачі ключовим є правильний вибір формули та одиниць вимірювання, адже помилка на цьому етапі може зіпсувати весь розрахунок. Давай розберемо, як обчислювати об’єм для різних фігур — від простих кубів до складних конічних форм.
Основні формули для об’єму: від куба до сфери
Щоб знайти об’єм, потрібно знати формулу, яка відповідає формі об’єкта. Ось найпоширеніші геометричні тіла та їхні формули, які стануть твоїми надійними помічниками.
- Куб: Об’єм куба — це просто добуток довжини його ребра в третьому ступені. Формула: V = a³, де a — довжина ребра. Наприклад, якщо ребро куба 4 см, то об’єм буде 4 × 4 × 4 = 64 см³. Легко, чи не так?
- Прямокутний паралелепіпед: Ця фігура схожа на коробку. Формула: V = a × b × c, де a, b, c — довжина, ширина та висота. Наприклад, для коробки 5 см × 3 см × 2 см об’єм дорівнює 5 × 3 × 2 = 30 см³.
- Циліндр: Об’єм циліндра залежить від площі його основи та висоти. Формула: V = π × r² × h, де r — радіус основи, h — висота, а π ≈ 3,14159. Якщо циліндр має радіус 2 см і висоту 10 см, об’єм буде 3,14159 × 2² × 10 ≈ 125,66 см³.
- Конус: Конус — це ніби циліндр, але з однією основою, що звужується до вершини. Формула: V = (1/3) × π × r² × h. Для конуса з радіусом 3 см і висотою 6 см об’єм буде (1/3) × 3,14159 × 3² × 6 ≈ 56,55 см³.
- Сфера: Сфера — це ідеально круглий об’єкт, як м’яч. Формула: V = (4/3) × π × r³. Для кулі з радіусом 5 см об’єм буде (4/3) × 3,14159 × 5³ ≈ 523,6 см³.
- Піраміда: Об’єм піраміди залежить від площі основи та висоти. Формула: V = (1/3) × S × h, де S — площа основи, h — висота. Наприклад, для піраміди з квадратною основою 4 см × 4 см і висотою 6 см об’єм буде (1/3) × (4 × 4) × 6 = 32 см³.
Ці формули — твій базовий арсенал. Але не поспішай: правильний вибір формули залежить від точного розуміння форми об’єкта. Якщо сумніваєшся, намалюй фігуру на папері — це допоможе!
Крок за кроком: як знайти об’єм у задачах
Обчислення об’єму здається складним лише на перший погляд. Насправді це захопливий процес, схожий на розгадування головоломки. Ось універсальний алгоритм, який працює для будь-якої фігури.
- Визнач форму об’єкта. Чи це куб, циліндр, чи щось складніше? Наприклад, акваріум зазвичай має форму паралелепіпеда, а бочка — циліндра.
- Збери всі дані. Знайди виміри: довжину, ширину, висоту, радіус тощо. Якщо даних немає, можливо, їх потрібно обчислити з інших параметрів (наприклад, діаметр можна поділити на 2, щоб знайти радіус).
- Вибери правильну формулу. Скористайся таблицею формул вище або перевір, чи є спеціальна формула для твоєї фігури.
- Підстав значення. Уважно підставляй числа у формулу. Переконайся, що всі одиниці вимірювання однакові (наприклад, усі в сантиметрах).
- Обчисли результат. Використовуй калькулятор для точності, особливо якщо працюєш із π або дробами.
- Перевір одиниці. Якщо завдання просить об’єм у літрах, а ти отримав см³, пам’ятай: 1000 см³ = 1 л.
Цей алгоритм — твій надійний провідник. Наприклад, щоб знайти об’єм акваріума 50 см × 30 см × 40 см, визначаємо, що це паралелепіпед, використовуємо формулу V = a × b × c, підставляємо значення: 50 × 30 × 40 = 60 000 см³, або 60 літрів. Готово!
Приклад із життя: об’єм басейну
Уяви, що ти хочеш наповнити круглий басейн водою. Його діаметр 4 м, а глибина 1,5 м. Як знайти об’єм? Спершу визначаємо, що басейн — це циліндр. Радіус = діаметр ÷ 2 = 4 ÷ 2 = 2 м. Формула: V = π × r² × h. Підставляємо: 3,14159 × 2² × 1,5 ≈ 18,85 м³. Отже, тобі знадобиться приблизно 18 850 літрів води! Такі розрахунки допомагають планувати витрати та економити час.
Типові помилки при обчисленні об’єму
Помилки в обчисленні об’єму — це як камінці на шляху: їх легко обійти, якщо знати, де вони лежать. Ось найпоширеніші пастки та як їх уникнути.
Типові помилки 🚨
- Неправильні одиниці вимірювання. Якщо довжина в метрах, а висота в сантиметрах, результат буде хаотичним. Завжди переводь усі виміри в одну систему перед розрахунком.
- Плутанина з формулами. Наприклад, використання формули циліндра для конуса призведе до завищеного результату, адже конус має лише третину об’єму циліндра з такими ж параметрами.
- Неточне значення π. Для простих розрахунків бери π ≈ 3,14, але для точних — π ≈ 3,14159. У шкільних задачах уточнюй вимоги вчителя.
- Неправильне округлення. Якщо завдання вимагає округлення до двох знаків після коми, не залишай три — це може коштувати балів.
- Пропуск множника. У формулах на кшталт V = (1/3) × S × h легко забути про “1/3”, що повністю змінить результат.
Щоб уникнути цих помилок, завжди перевіряй свої розрахунки двічі та малюй схему об’єкта. Це не лише економить час, а й додає впевненості!
Об’єм складних фігур: як впоратися?
Іноді об’єкти мають нестандартну форму, і стандартні формули не підходять. Наприклад, як знайти об’єм вази з круглою основою, що звужується догори, або скульптури? Ось кілька підходів для складних випадків.
- Розбиття на прості фігури. Складну форму можна розкласти на простіші: циліндри, конуси, паралелепіпеди. Наприклад, бак для води може складатися з циліндра та півсфери зверху. Обчисли об’єм кожної частини окремо і додай їх.
- Метод інтеграції. Для фігур із змінним перерізом (наприклад, вази) використовують інтегральне числення, обчислюючи об’єм через функцію площі перерізу. Це складніше, але для студентів вишів — цілком реально.
- Експериментальний метод. Якщо формулу знайти важко, виміряй об’єм рідиною. Наповни об’єкт водою і перелий її в мірну ємність. Наприклад, так можна визначити об’єм глечика (згідно з “Фізикою для школи”, автор О. Сиротюк).
Для складних об’єктів ключовим є творчий підхід. Якщо не впевнений, почни з наближення: оціни форму як комбінацію простих фігур, а потім уточнюй розрахунки.
Практичне застосування об’єму в житті
Об’єм — це не лише шкільні задачі, а й реальні виклики, які ми зустрічаємо щодня. Ось як знання об’єму допомагають у різних сферах.
| Сфера | Приклад застосування |
|---|---|
| Будівництво | Розрахунок об’єму бетону для фундаменту (наприклад, 2 м × 3 м × 0,5 м = 3 м³). |
| Кулінарія | Визначення об’єму форми для випічки, щоб тісто не перелилось. |
| Транспорт | Розрахунок об’єму вантажного відсіку для перевезення речей. |
| Екологія | Оцінка об’єму водойм для планування очищення (згідно з “Екологія”, автор М. Білик). |
Джерело: адаптовано з підручників “Фізика для школи” (О. Сиротюк) та “Екологія” (М. Білик).
Знання об’єму допомагає економити ресурси, планувати роботу та навіть берегти природу. Наприклад, розрахувавши об’єм бака для дощової води, ти можеш зібрати більше води для поливу саду!
Поради для легшого запам’ятовування формул
Формули об’єму можуть здаватися складними, але з правильним підходом вони стануть твоїми друзями. Ось кілька трюків, щоб їх запам’ятати.
- Візуалізуй. Уяви куб як коробку, циліндр як банку, а конус як морозиво в ріжку. Асоціації допомагають!
- Групуй формули. Зверни увагу: формули для конуса та піраміди мають множник “1/3”, бо вони “звужуються” порівняно з циліндром чи призмою.
- Практикуйся. Розв’яжи 3–5 задач для кожної формули, і вони закарбуються в пам’яті.
- Використовуй мнемонічні правила. Наприклад, для сфери: “Чотири третини пі-ер-куб” — звучить як заклинання, але працює!
Ці поради зроблять навчання веселим і ефективним. Спробуй намалювати кожну фігуру та підписати формулу — це закріпить знання!