Основи: що таке чотирикутник і його кути
Чотирикутник — це плоска геометрична фігура, яка має чотири сторони та чотири кути. Уявіть собі аркуш паперу, складений у формі квадрата, прямокутника чи навіть трапеції — усі вони є чотирикутниками! Кути чотирикутника утворюються в точках, де його сторони перетинаються, і саме їхня сума викликає стільки запитань у школярів і любителів геометрії.
Чому сума кутів чотирикутника завжди однакова? Це не випадковість, а математичний закон, який можна довести кількома способами. У цьому розділі ми розберемо, звідки береться ця сума, і почнемо з головного: сума внутрішніх кутів будь-якого чотирикутника завжди дорівнює 360 градусів. Але як це працює? Давайте розбиратися!
Чому сума кутів чотирикутника дорівнює 360°
Щоб зрозуміти, чому сума кутів чотирикутника становить 360°, уявімо, що ми можемо “розібрати” чотирикутник на простіші частини. Один із найпростіших способів довести це — розділити чотирикутник на два трикутники.
Ось як це працює: проведіть діагональ із одного кута чотирикутника до протилежного. Наприклад, у чотирикутнику ABCD з’єднайте точки A і C. Це розділить фігуру на два трикутники: ABC і ADC. Ми знаємо, що сума кутів у будь-якому трикутнику дорівнює 180° (згадайте шкільну теорему про суму кутів трикутника). Оскільки чотирикутник складається з двох таких трикутників, загальна сума кутів буде: 180° + 180° = 360°.
Цей метод не лише простий, але й універсальний. Він працює для будь-якого чотирикутника — будь то квадрат, ромб чи навіть неправильна фігура зі сторонами різної довжини. Щоб закріпити це, розглянемо ще один спосіб доведення.
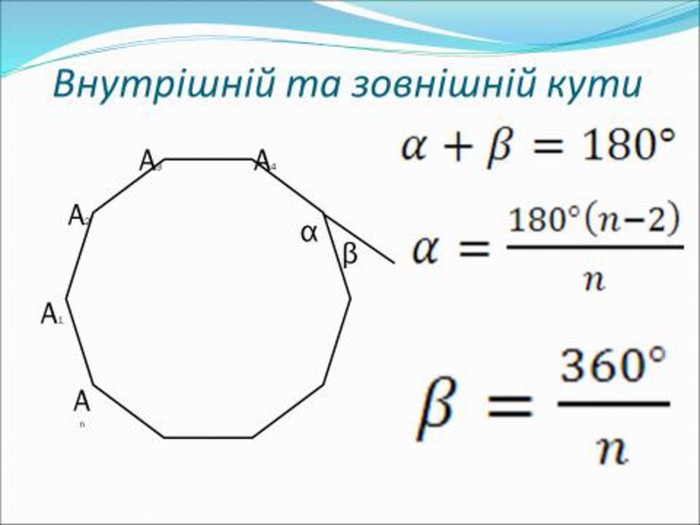
Доведення через зовнішні кути
Інший цікавий підхід — використати зовнішні кути чотирикутника. Зовнішній кут у вершині чотирикутника — це кут, утворений однією стороною та продовженням іншої сторони. Наприклад, у вершині A чотирикутника ABCD зовнішній кут утворюється між стороною AB і продовженням сторони DA.
Цікаво, що сума зовнішніх кутів будь-якого багатокутника, включно з чотирикутником, завжди дорівнює 360°, незалежно від кількості сторін. Для чотирикутника це означає, що сума його зовнішніх кутів (по одному на кожну вершину) становить 360°. Оскільки внутрішній і зовнішній кути в кожній вершині доповнюють один одного до 180°, можна математично пов’язати їх із внутрішніми кутами, але ключовий висновок той самий: внутрішні кути чотирикутника в сумі дають 360°.
Види чотирикутників і їхні кути
Не всі чотирикутники однакові, і це додає темі пікантності! Різні типи чотирикутників мають свої особливості, але сума їхніх кутів завжди залишається 360°. Давайте розглянемо найпоширеніші види чотирикутників і те, як їхні кути поводяться.
Ось основні типи чотирикутників, які варто знати:
- Квадрат: Усі чотири кути дорівнюють 90°. Перевірмо: 90° + 90° + 90° + 90° = 360°. Усе сходиться! Квадрат — це ідеальний приклад чотирикутника, де кожен кут чітко визначений.
- Прямокутник: Як і в квадраті, усі кути прямокутника — прямі, тобто 90°. Сума: 90° × 4 = 360°. Прямокутник схожий на квадрат, але його сторони можуть мати різну довжину.
- Ромб: У ромба протилежні кути рівні, але вони не обов’язково прямі. Наприклад, два кути можуть бути 60°, а два інші — 120°. Перевірка: 60° + 120° + 60° + 120° = 360°.
- Трапеція: У трапеції кути можуть бути різними, але їхня сума все одно дорівнює 360°. Наприклад, у рівнобедреній трапеції кути при основі можуть бути 70°, а два інші — 110°. Сума: 70° + 70° + 110° + 110° = 360°.
- Паралелограм: Протилежні кути паралелограма рівні, а сусідні кути доповнюють один одного до 180°. Наприклад, якщо один кут 70°, то протилежний також 70°, а два сусідні — по 110°. Сума: 70° + 110° + 70° + 110° = 360°.
- Неправильний чотирикутник: Це чотирикутник, у якого сторони та кути не мають чіткої симетрії. Наприклад, кути можуть бути 80°, 100°, 90° і 90°. Сума: 80° + 100° + 90° + 90° = 360°.
Як бачите, незалежно від типу чотирикутника, сума кутів завжди дорівнює 360°. Ця універсальність робить геометрію такою захопливою —thesauruses!
Як знайти невідомий кут чотирикутника
Часто в задачах потрібно знайти значення одного або кількох кутів чотирикутника, знаючи решту. Це простіше, ніж здається! Оскільки сума кутів чотирикутника завжди 360°, ми можемо використати цю інформацію для обчислень.
Ось покроковий алгоритм, як знайти невідомий кут:
- Визначте відомі кути: Зберіть інформацію про всі відомі кути чотирикутника. Наприклад, у вас є три кути: 80°, 90° і 110°.
- Відніміть від 360°: Від загальної суми кутів (360°) відніміть суму відомих кутів: 360° − (80° + 90° + 110°) = 360° − 280° = 80°.
- Перевірте результат: Переконайтеся, що отриманий кут має сенс у контексті чотирикутника. Наприклад, якщо це квадрат, усі кути мають бути 90°.
Цей метод працює для будь-якого чотирикутника, але для спеціальних типів (наприклад, паралелограма чи трапеції) можуть бути додаткові умови, як-от рівні протилежні кути чи кути, що доповнюють один одного до 180°.
Практичне застосування суми кутів чотирикутника
Знання суми кутів чотирикутника — це не просто шкільна теорія. Воно має реальне застосування в архітектурі, дизайні, інженерії та навіть комп’ютерній графіці.
Ось кілька прикладів, де це корисно:
- Архітектура: При проєктуванні будівель архітектори використовують чотирикутники (наприклад, прямокутники чи трапеції) для створення стійких конструкцій. Розуміння кутів допомагає забезпечити правильну геометрію.
- Комп’ютерна графіка: У 3D-моделюванні чотирикутники (так звані “квади”) є основою для створення поверхонь. Кути впливають на те, як модель виглядає на екрані.
- Робототехніка: У навігації роботів чотирикутники використовуються для побудови карт і визначення траєкторій руху.
Ці приклади показують, що геометрія чотирикутників — це не лише абстрактна математика, а й інструмент, який допомагає створювати реальний світ навколо нас.
Цікаві факти по темі: 🧠✨
Чотирикутники — це не лише нудні формули! Ось кілька захопливих фактів, які зроблять геометрію цікавішою:
- Чотирикутники в природі: У природі чотирикутники зустрічаються рідше, ніж трикутники, але їх можна побачити в кристалах солі (кубічна структура) чи в деяких листках рослин.
- Тесселяція: Чотирикутники, як-от квадрати чи прямокутники, ідеально підходять для тесселяції — заповнення площини без прогалин. Саме тому плитка на підлозі часто має форму чотирикутника!
- Чотирикутники в мистецтві: Художники епохи Відродження, такі як Леонардо да Вінчі, використовували геометрію чотирикутників для створення перспективи в картинах.
- Незвичайні чотирикутники: Існують так звані “самоперетинні” чотирикутники, де сторони перетинаються, утворюючи зіркоподібні фігури. Їхня сума кутів може відрізнятися від 360°!
Ці факти показують, що чотирикутники — це не лише математика, а й частина нашого світу, від природи до мистецтва!
Типові задачі та як їх розв’язати
Щоб закріпити знання, розглянемо кілька типових задач, які часто зустрічаються в шкільних підручниках чи на іспитах.
Ось приклади задач і їхнє розв’язання:
| Задача | Розв’язання |
|---|---|
| У чотирикутнику три кути дорівнюють 70°, 80° і 120°. Знайдіть четвертий кут. | Сума кутів = 360°. Сума відомих кутів: 70° + 80° + 120° = 270°. Четвертий кут: 360° − 270° = 90°. |
| У паралелограмі один кут дорівнює 65°. Знайдіть усі кути. | У паралелограмі протилежні кути рівні, а сусідні доповнюють до 180°. Отже, два кути = 65°, а два інші: 180° − 65° = 115°. Кути: 65°, 115°, 65°, 115°. |
Джерело: Основано на стандартних задачах із підручника “Геометрія 7–9 класи” (автор: Мерзляк А. Г.).
Ці задачі допомагають не лише зрозуміти теорію, а й навчитися застосовувати її на практиці. Спробуйте розв’язати кілька подібних прикладів самостійно!
Чому важливо розуміти суму кутів
Розуміння суми кутів чотирикутника — це не лише спосіб здати іспит. Це ключ до глибшого сприйняття геометрії, яка лежить в основі багатьох наук і технологій. Коли ви знаєте, що сума кутів завжди 360°, ви можете передбачити поведінку фігур, створювати точні креслення чи навіть проєктувати будівлі.
Більше того, геометрія вчить логічного мислення. Кожен доказ, кожна задача — це маленький пазл, який тренує ваш мозок. А ще це просто красиво! Є щось магічне в тому, як числа та кути завжди сходяться в ідеальній гармонії.
Поради для вивчення геометрії чотирикутників
Геометрія може здаватися складною, але з правильним підходом вона стає захопливою. Ось кілька порад, як опанувати тему чотирикутників:
- Малюйте: Завжди кресліть чотирикутник на папері. Візуалізація допомагає зрозуміти, як кути пов’язані між собою.
- Розбивайте на трикутники: Якщо задача складна, проведіть діагональ і розв’яжіть її для двох трикутників.
- Практикуйтесь: Розв’язуйте якомога більше задач. Чим більше прикладів ви побачите, тим краще зрозумієте закономірності.
- Використовуйте технології: Програми на кшталт GeoGebra дозволяють експериментувати з чотирикутниками в інтерактивному режимі.
Ці поради допоможуть вам не лише зрозуміти суму кутів, а й полюбити геометрію. Пам’ятайте: кожна задача — це пригода, де ви відкриваєте щось нове!